Outómato fenito

Ua máquina de stados fenitos (FSM - de l'anglés Finite State Machine) ó outómato fenito ye un modelo matemático ousado para repersentar porgramas de cumputadores ó circuitos lógicos. L cunceito ye cuncebido cumo ua máquina abstrata que debe star nun de sous fenitos stados. La máquina stá an solo un stado por beç, este stado ye chamado de estado atual. Un stado armazena anformaçones subre l passado, esto ye, el reflete las mudanças zde l'antrada nun stado, ne l'ampeço de l sistema, até l momiento persente. Ua trasiçon andica ua mudança de stado i ye çcrita por ua cundiçon que percisa ser rializada para que la trasiçon ocorra. Ua açon ye la çcriçon dua atebidade que debe ser rializada nun detreminado momiento.

Máquinas de stado fenito puoden modelar un grande númaro de porblemas, antre ls quales l'outomaçon de zeign eiletrónico, porjeto de protocolo de quemunicaçon, análeze i outras aplicaçones d'angenharie. Na biologie i na pesquisa de la anteligéncia artificial, máquinas de stado ó hierarquias de máquinas de stado son, por bezes, outelizadas para çcrebir sistemas neurológicos i an lenguística para çcrebir las gramáticas de las lenguaiges naturales.

Cunceitos i Bocabulário[eiditar | eiditar código-fuonte]

Un stado çcribe un nuolo de cumportamiento de l sistema an que stá a la spera dua cundiçon para eisecutar ua trasiçon. Normalmente, un stado ye antroduzido quando l sistema nun reage de la mesma forma para ua mesma cundiçon. Ne l'eisemplo dun sistema de rádio de carro, quando se stá oubindo ua staçon de rádio, l'estímulo "próssimo" senefica ir pa la próssima staçon. Mas quando l sistema stá ne l stado de CD, l'estímulo "próssimo" senefica ir pa la próssima faixa. L mesmo stímulo zamcadeia açones defrentes, dependendo de l stado atual. An alguas repersentaçones de stado fenito máquina, tamien ye possible associar açones a un stado:

Açon d'antrada: l que ye rializado al antrar ne l'estado,
Açon de salida: l que ye eisecutado al salir de l stado.

La trasiçon ye un cunjunto d'açones la séren eisecutadas quando ua cundiçon fur cumprida ó quando un eibento ye recebido. Máquinas de stado son outelizadas para çcrebir circuitos sequenciales. Defrentemente dun cuntador qu'an giral cunta eibentos, ua máquina de stado questuma ser ousada para cuntrolar l'eibento.

La máquina stá an solo un stado por beç, este stado ye chamado d'estado atual. Un stado armazena anformaçones subre l passado, esto ye, el reflete las mudanças zde l'antrada nun stado, ne l'ampeço de l sistema, até l momiento persente. Ua trasiçon andica ua mudança de stado i ye çcrita por ua cundiçon que percisa ser rializada para que la trasiçon ocorra. Ua açon ye la çcriçon dua atebidade que debe ser rializada nun detreminado momiento.

Repersentaçon[eiditar | eiditar código-fuonte]

Fig. 1 Eisemplo de máquina de stados SDL

Diagrama de stados[eiditar | eiditar código-fuonte]

Máquinas de stados fenitos puoden ser repersentadas por meio dun diagrama de stados (ó diagrama de trasiçon de stados). Dibersas tabelas de trasiçon de stados son ousadas, la mais famosa ye la mostrada ambaixo. La cumbinaçon de l stado atual (s: B) cun ua cundiçon (s: Y) detremina l próssimo stado (s: C). Atrabeç de l'uso de las tabelas podemos repersentar ua de máquina fenita de stados que cuntenha anformaçones cumpletas subre las açones.

Tabela de trasiçon de stados
Stado Atual → Cundiçon ↓	Stado La	Estado B	Stado C
Cundiçon X	...	...	...
Cundiçon Y	...	Estado C	...
Cundiçon Z	...	...	...

Máquinas de stados UML[eiditar | eiditar código-fuonte]

La UML ten ua notaçon para çcrebir máquinas de stado. Máquinas de stado UML supírun las lemitaçones de las FSMs tradecionales, mantendo ls sous percipales benefícios. Máquinas de stados UML antroduzen ls nuobos cunceitos de stados amarrados hierarquicamente i regiones ortogonales, anquanto stende la noçon d'açones. Máquinas de stado UML ténen las caratelísticas d'ambas las máquinas de Mealy i More. Eilhas suportan açones que dependen tanto de l stado de l sistema quanto de la cundiçon, cumo an máquinas de Mealy, assi cumo açones d'antrada i salida que stan associadas culs stados an beç de trasiçones, cumo an máquinas de More.

Máquinas de stados SDL[eiditar | eiditar código-fuonte]

La SDL ye un padron de la Ounion Anternacional de Telecomunicaçones i ye ua de las melhores lenguaiges para çcrebir máquinas de stado, pus anclui simblos gráficos para çcrebir las açones na trasiçon:

ambiar un eibento
recebir un eibento
ampeçar un temporizador
cancelar un temporizador
ampeçar ua nuoba máquina de stado simultánea
decison

SDL ancorpora tipos básicos de dados chamado Abstrat Data Types, ua lenguaige d'açon, i ua semántica d'eisecuçon, la fin de tornar la máquina de stados fenitos eisecutable. Un eisemplo ye bisto na figura 1.

Outros diagramas de stado[eiditar | eiditar código-fuonte]

Eesisten bárias outras maneiras de se repersentar ua FSM, assi cumo mostrado na figura 2.

Un eisemplo ye l HDL:

An HDL (Hardware Çcrition Language) ó LDH(Lengugen de Çcriçon de Hardware) ye possible criar máquinas de stado simples i de çcriçon antuitiba. Ye feito l'uso de stados nomeados pa ls quales nun hai balores binairos defenidos. An BHDL eisisten las palabras-chabe cumo TYPE por eisemplo, que define l tipo enumerado an BHDL. L porjetista lista an nomes simbólicos (defrentes de las palabras-chabe) todos ls possibles balores qu'un senhal, bariable ó porto que ye declarado cumo sendo deste tipo puode assumir. L balor binairo ye detreminado pul cumpilador, deixando l trabalho de l porjetista mais simples.

Uso[eiditar | eiditar código-fuonte]

Para alhá de sou uso na modelaige de sistemas reatibos eiqui apersentados, outómatos de stados fenitos son seneficatibos an dibersas árias, ancluindo angenharie eilétrica, lenguística, ciéncia de la cumputaçon, filosofie, biologie, matemática i lógica. Máquinas de stados fenitos son ua classe d'outómatos studada na teorie de ls outómatos i teorie de la cumputaçon. An ciéncia de la cumputaçon, máquinas de stados fenitos son amplamente outelizados na modelaige de l cumportamiento de l'aplicatibo, zeign de sistemas digitales d'hardware, angenharie de software, cumpiladores, protocolos de rede, i l studo de la cumputaçon i lenguaiges.

Classeficaçon[eiditar | eiditar código-fuonte]

Eesisten dous grupos: Aceitadores/Reconhecedores i Trasdutores.

Aceitadores i reconhecedores[eiditar | eiditar código-fuonte]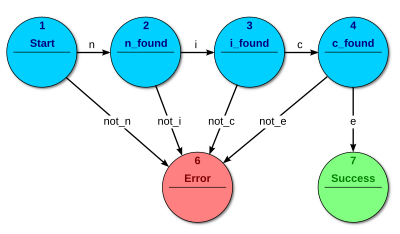

Aceitadores i reconhecedores porduzen ua salida binária, dezindo si ó nun para respunder se l'antrada ye aceita pula máquina ó nó. Todos ls stados de l FSM stan a dezir se quier aceitar ó nun quier aceitar. Ne l momiento an que todas las antradas son processadas, se l stado atual ye un estado d'aceitaçon, l'antrada ye aceita, causo cuntrairo ye rejeitada. Cumo regra l'antrada son simblos (carateres); açones nun son ousadas. L'eisemplo de la figura 3 mostra ua máquina de stados fenitos qu'aceita la palabra "nice". Neste FSM l único stado d'aceitaçon ye l númaro 7.

La máquina tamien puode ser çcrita cumo la defeniçon dua lenguaige, que cunterie todas las palabras aceitas pula máquina i nanhue de las que son rejeitadas; dezimos anton que la lenguaige ye aceita pula máquina. Por defeniçon, lenguaiges aceitas por FSMs son las lenguaiges regulares, esto ye, ua lenguaige ye regular se eisiste algua FSM que l'aceita.

Stado Einicial[eiditar | eiditar código-fuonte]

L stado enicial ye giralmente mostrado zenhando ua seta "apuntando para el a partir de qualquiera lugar" (Sipser (2006) p. 34).

Stados d'aceitaçon (ó Stados Finales)[eiditar | eiditar código-fuonte]

Fig. 4: Repersentaçon dua FSM. Este eisemplo mostra ua FSM que detremina se un númaro binairo ten un númaro par ó ímpar de 0's, adonde S₁ ye un **stado d'aceitaçon**.

Stados d'aceitaçon son aqueilhes an que la máquina relata que la sequéncia d'antrada, cumo processadas até agora, ye nembro de la lenguaige qu'eilha aceita. Ye giralmente repersentado por un círclo duplo. Un eisemplo dun stado d'aceitaçon aparece na figura 4: un outómato fenito determinístico (AFD) que deteta se la sequéncia d'antrada binária cuntén un númaro par de 0's. S₁ (que tamien ye l stado enicial) andica l'estado ne l qual un númaro par de 0's fui dado na antrada. S₁ ye, antoce, un stado d'aceitaçon. Esta máquina bai treminar nun stado d'aceitaçon se la sequéncia binária cuntén un númaro par de 0's (ancluindo qualquiera sequéncia binária que nun cuntenhan 0's). Eisemplos de cadeias aceitas por este AFD son: eipsilon (la cadeia bazie), 1, 11, 11 ..., 00, 010, 1010, 10110, etc.

Trasdutores[eiditar | eiditar código-fuonte]

Trasdutores gírun ua salida baseada nua antrada i/ó un stado outelizando açones. Eilhes son outelizados para aplicaçones de cuntrole.

La salida porduzida por un cuntador ó ua máquina de stado puode benir diretamente de las salidas de l flip-flop, ó alguns circuitos lógicos. Las dues bariaçones son chamadas de modelo Mealy de circuitos sequencial i modelo More.

Ne l modelo Mealy, ls senhales de salida tamien son cuntrolados por senhales d'antrada adicionales, anquanto l modelo More nun ten nanhun cuntrole sternos pa ls senhales de salida gerados.La salida de l modelo More ye funçon solo de l stado atual de l flip-flop.

Las salidas dun circuito de tipo More seran cumpletamente síncronas an relaçon al clock de l circuito, anquanto salidas porduzidas por un circuito de tipo Mealy puoden mudar assincronamente.

Máquina de More: La FSM outeliza solo açones d'antrada, i.i. la salida depende solamente de l stado. La bantaige de l modelo de More ye la simplificaçon de l cumportamiento. Cunsidremos por eisemplo ua FSM de More dua puorta d'eilebador cun 4 stados "Abierta", "Cerrada", "Abrindo", "Fechando". La máquina de stados reconhece dous comandos: "comando_abrir" i "comando_ancerrar" que çpórun l'altaraçon de stado. L'açon d'antrada (I:) ne l'estado "Abrindo" liga l motor qu'abre la puorta, l'açon d'antrada ne l stado "Fechando" liga l motor na outra direçon, fechando la puorta. Ls stados "Abierta" i "Cerrada" nun zampenhan nanhue açon. Eilhes sinalizan pa l mundo sterno (i.g. para outras máquinas de stado) la situaçon: "puorta stá abierta" ó "puorta stá cerrada".

Máquina de Mealy: La FSM outeliza solo anput ationes, i.i. la salida depende de l'antrada i de l stado. L'uso dua FSM de Mealy normalmente lieba a ua reduçon ne l númaro de stados. Por eisemplo ua FSM de Mealy amplementando l mesmo cumportamiento bisto ne l'eisemplo de More (l cumportamiento depende ne l modelo d'eisecuçon amplementado na FSM i eirá funcionar i.g. para ua FSM birtual mas nun para ua FSM d'eibentos dirigidos). Eesisten dues anput ationes(I:): “ampeçe l motor para ancerrar la puorta se l comando_ancerrar (sensor_closed na figura 5) chegar” i “ampeçe l motor na direçon ouposta para abrir la puorta se l comando_abrir (sensor_oupened na figura 5) chegar”.

Na prática modelos mistos son mui outelizados.

Mais detalhes subre las defrenças i usos de ls modelos de More i Mealy, ancluindo un eisemplo eisecutable, puoden ser ancontrados na nota técnica sterna .com/atibe/cuntent/en/technology/technical_notes.php#tn10 "Modelo de More ó Mealy?"^{[lhigaçon einatiba]}(decumiento an anglés)

Determenismo[eiditar | eiditar código-fuonte]

Ua çtinçon adicional stá antre outómato determinístico (AFD) i nó-determinístico (AFN). Ne l'outómato determinístico, para cada stado hai satamente ua trasiçon para cada antrada possible. Ne l'outómato nun determinístico, puode haber nanhue, ua ó mais dua trasiçon dun detreminado stado para ua antrada possible.

La FSM cun solo un stado ye chamada de FSM cumbinatória i outeliza solo anput ationes. Este cunceito ye útele quando un númaro de FSM dében trabalhar juntas, i adonde ye cumbeniente cunsidrar ua parte puramente cumbinatória cumo ua forma de FSM para se adequar a las ferramientas de porjeto.

Semánticas Altarnatibas[eiditar | eiditar código-fuonte]

Hai outros cunjuntos de semántica çponible para repersentar máquinas de stado. Por eisemplo, eisisten ferramientas para modelaige i lógica para porjetar cuntroladores ancorporados.^[1] Eilhes cumbinan máquinas de stado hierárquico, gráficos de fluxo i tabelas de berdade para ua lenguaige, resultando nun defrente formalismo i cunjunto de semántica.^[2] La Figura 6 eilustra esta mistura de máquinas de stado i gráficos de fluxo cun un cunjunto de stados para repersentar l stado dun cronómetro i un gráfico de fluxo para cuntrolar ls tiques de l reloijo. Estes gráficos, cumo máquinas de stado ouriginales de Harel,^[3] apoian ls stados hierarquicamente amarrados, regiones ortogonales, açones de l stado, i las açones de trasiçon.^[4]

Lógica de la FSM[eiditar | eiditar código-fuonte]

L próssimo stado i la salida dua FSM son ua funçon de l'antrada i de l'atual stado. La lógica de la FSM ye mostrada na figura 6.

Modelo matemático[eiditar | eiditar código-fuonte]

Dependendo de l tipo puoden haber bárias defeniçones.

Ua máquina de stados fenitos tipo aceitador ye ua quíntupla <Σ, S, s₀, δ, F>, adonde:

Σ ye l'alfabeto d'antrada (un cunjunto de simblos fenitos nun bazio),
S ye un cunjunto fenito de stados nun bazio,
s₀ ye l stado enicial, un eilemiento de S,
δ ye la funçon de trasiçon de stados: δ: S x Σ → S (nun AFN, serie δ: S x Σ → P(S), esto ye, δeirie retornar un cunjunto d'estados),
F ye l cunjunto de stados finales, un (possiblemente bazio) subconjunto de S.

Para ambos ls FSMs determinísticas i nó-determenistica, ye cumbencional para permitir δ ser ua funçon parcial, ó seia, δ(q, x) nun ten que ser defenida para cada cumbinaçon de q $\in$ S i x $\in$ Σ. Se ua FSM M stá nun stado q, l simblo seguinte ye x i δ(q, x) nun stá defenida, anton M puode anunciar un erro (ó seia, rejeitar l'antrada). Esso ye útele an defeniçones de máquinas de stado an giral, mas menos útele al trasformar la máquina. Alguns algoritmos an sue forma padron puoden eisigir funçones totales.

Ua máquina de stados fenitos ye ua máquina de Turing restrita an que la cabeça solo puode "ler" las ouparaçones, i siempre se mobe de la squierda pa la dreita.^[5]

Ua máquina de stados fenitos tipo trasdutor ye ua séxtupla <Σ, Γ, S, s₀, δ, ω>, adonde:

Σ ye l'alfabeto d'antrada (un cunjunto de simblos fenitos nun bazio),
Γ ye l'alfabeto de salida (un cunjunto de simblos fenitos nun bazio),
S ye un cunjunto fenito de stados nun bazio,
s₀ ye l stado enicial, un eilemiento de S,
δ ye la funçon de trasiçon de stados: δ: S x Σ → S (nun AFN, serie δ: S x Σ → P(S), esto ye, δeirie retornar un cunjunto d'estados),
ω ye la funçon de salida.

Se la funçon de salida ye ua funçon de l stado i de l'alfabeto d'antrada (ω: S x Σ → Γ )essa defeniçon corresponde al modelo de Mealy. Se la funçon de salida depende solamente de l stado (ω: S → Γ ) essa defeniçon corresponde al modelo de More.

Se çcunsiderarmos l simblo purmeira salida dua máquina de More, ω(s₀), anton eilha puode ser facilmente cumbertida nua máquina de Mealy de salida eiquibalente defenindo la funçon de salida de cada trasiçon de la de Mealy (esto ye, rotulando cada stremidade) cul simblo de salida dado al stado de çtino de la de More. La trasformaçon ambersa ye menos simples, porque un stado de la máquina de Mealy puode tener rótulos de salida defrentes an sues trasiçones d'antrada (stremidades). Cada stado ten de ser debedido an bários stados de la máquina de More, ua para cada simblo de salida ancidente.^[6]

Teoria de autômatos: linguagem formal e gramática formal
Hierarquia Chomsky	Gramática	Linguagem	Reconhecedor
Tipo-0	Irrestrita	Recursivamente enumerável	Máquina de Turing
--	--	Recursiva	Máquina de Turing que sempre para
Tipo-1	Sensível ao contexto	Sensível ao contexto	Autômato linearmente limitado
Tipo-2	Livre de contexto	Livre de contexto	Autômato com pilha
Tipo-3	Regular	Regular	Autômato finito

Amplementaçon[eiditar | eiditar código-fuonte]

Aplicaçones de Hardware[eiditar | eiditar código-fuonte]

Nun circuito digital, ua FSM puode ser custruída outelizando un çpositibo lógico porgramable. Un cuntrolador lógico porgramable, puortas lógicas i flip-flops ó relays. Mais specificamente, l'amplementaçon d'hardware requer un registrador para armazenar l stado de las bariables, un bloco de lógica cumbinacional que detremina l stado de trasiçon i un segundo bloco de lógica cumbinacional que detremina la salida de la FSM.

L mais famoso ye l cuntrolador de Richards

Máquinas de Mealy i de More porduzen lógica cun salida assíncrona, porque hai un atraso de propagaçon antre l flip-flop i salida. Esso causa frequéncias mais lentas ouperando na FSM. Ua máquina de Mealy ó de de More puode ser cumbertida para ua FSM tal qual la salida ye diretamente dun flip-flop, l que faç la FSM funcionar an frequéncias mais altas. Este tipo de FSM ye chamado a las bezes FSM de Medbedeb.^[7] Un cuntador ye la forma mais simples desse tipo de FSM.

Aplicaçones de Software[eiditar | eiditar código-fuonte]

Ls seguintes cunceitos son quemumente ousados para custruir aplicaçones de software cun máquinas de stados fenitos:

Porgramaçon baseada an outómatos
FSM ourientada a eibentos
FSM Birtual (BFSM)

Refréncias[eiditar | eiditar código-fuonte]

↑ .com/users/tiwari/papers/stateflow.pdf Tiwari, La. (2002). Formal Semantics and Analysis Methods fur Simulink Stateflow Models.^{[lhigaçon einatiba]}
↑ Hamon, G. (2005). La Denotational Semantics fur Stateflow. Anternational Cunference on Ambedded Software (pp. 164–172). Jersey City, NJ: ACM.^{[lhigaçon einatiba]}
↑ Harel, D. (1987). La Bisual Formalisn fur Cumplex Systems. Science of Cumputer Porgramming , 231–274.^{[lhigaçon einatiba]}
↑ Alur, R., Kanade, La., Ramesh, S., & Shashidhar, K. C. (2008). Symbolic analysis fur amprobing simulation coberage of Simulink/Stateflow models. Anternation Cunference on Ambedded Software (pp. 89–98). Atlanta, GA: ACM.^{[lhigaçon einatiba]}
↑ Black, Paul I (12 May 2008). «Finite State Machine». U.S. National Anstitute of Standards and Technology. Ditionary of Algorithms and Data Strutures Cunsulte data an: |data= (ajuda)^{[lhigaçon einatiba]}
↑ .com/books?id=ikS8BLdLDxIC&pg=PA105 Outomata theory with modern applicationes Cunsulte valor |url= (ajuda). [S.l.]: Cambridge University Press. 2006. pp. 105–108. ISBN 9780521848879 ^{[lhigaçon einatiba]}
↑ «FSM: Medbedeb»

Timothy Kan, Synthesis of Finite State Machines: Funtional Outimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
Tiziano Billa, Synthesis of Finite State Machines: Logic Outimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
Carroll, J., Long, D. , Theory of Finite Outomata with an Antrodution to Formal Languages. Prentice Preça de casa. Anglewod Cliffs, 1989.
Hopcroft, J.I., Ullman, J.D., Antrodution to Outomata Theory, Languages and Cumputation. Addison -Wesley, 1979.
Kohabi, Z., Switching and Finite Outomata Theory. McGraw-Hill, 1978.
Gill, La., Antrodution to the Theory of Finite-state Machines. McGraw-Hill, 1962.
Cassandras, C., Lafortune, S., "Antrodution to Çcrete Eibent Systems". Kluwer, 1999, ISBN 0-7923-8609-4
Toci, Ronald J., "Sistemas digitales:Percípios i aplicaçones.", 10ª eidiçon, 2007

Links sternos[eiditar | eiditar código-fuonte]

Çcrition fron the Fre On-Line Ditionary of Cumputing^{[lhigaçon einatiba]}
NIST Ditionary of Algorithms and Data Strutures antry^{[lhigaçon einatiba]}
Hierarchical State Machines^{[lhigaçon einatiba]}

[1] .com/users/tiwari/papers/stateflow.pdf Tiwari, La. (2002). Formal Semantics and Analysis Methods fur Simulink Stateflow Models.^{[lhigaçon einatiba]}

[2] Hamon, G. (2005). La Denotational Semantics fur Stateflow. Anternational Cunference on Ambedded Software (pp. 164–172). Jersey City, NJ: ACM.^{[lhigaçon einatiba]}

[3] Harel, D. (1987). La Bisual Formalisn fur Cumplex Systems. Science of Cumputer Porgramming , 231–274.^{[lhigaçon einatiba]}

[4] Alur, R., Kanade, La., Ramesh, S., & Shashidhar, K. C. (2008). Symbolic analysis fur amprobing simulation coberage of Simulink/Stateflow models. Anternation Cunference on Ambedded Software (pp. 89–98). Atlanta, GA: ACM.^{[lhigaçon einatiba]}

[5] Black, Paul I (12 May 2008). «Finite State Machine». U.S. National Anstitute of Standards and Technology. Ditionary of Algorithms and Data Strutures Cunsulte data an: |data= (ajuda)^{[lhigaçon einatiba]}

[AndersonHead2006-6] .com/books?id=ikS8BLdLDxIC&pg=PA105 Outomata theory with modern applicationes Cunsulte valor |url= (ajuda). [S.l.]: Cambridge University Press. 2006. pp. 105–108. ISBN 9780521848879 ^{[lhigaçon einatiba]}

[7] «FSM: Medbedeb»

[1]

[2]

[3]

[4]

[5]

[6]

[7]